In earlier blogs, we explored the basic structure of neural networks. Now, let’s deep dive into how these concepts are implemented mathematically. The fundamental of neural network’s implementation is the field of linear algebra. Let’s break this down step by step.
Layers of a Neural Network
A neural network consists of multiple layers, each responsible for different aspects of data processing. The layers can be categorized as follows:
A neural network operates through interconnected layers, each contributing to data transformation:
- Input Layer
- This is the first layer, where the network interacts with external data.
- It accepts raw inputs, such as numerical values, images, or text, and passes them to subsequent layers for processing.
- Hidden Layers
- Hidden layers are the core computational engines of the network.
- These layers extract features and patterns by taking weighted inputs, applying biases, and using activation functions to introduce non-linearity.
- The number of hidden layers and neurons in each layer determine the network’s depth and capacity to model complex relationships.
- Output Layer
- The final layer, responsible for producing the network’s output.
- The structure of this layer depends on the task:
- For regression, it has a single neuron.
- For classification, it may have multiple neurons with probabilities assigned to each class (e.g., using the Softmax function).
These layers work together to process raw inputs, learn from patterns, and generate meaningful predictions, enabling neural networks to handle tasks ranging from image recognition to financial forecasting.
The Role of Mathematics
To implement these layers computationally, we rely on vectors and matrices.
-
Vectors:
- A vector is a fundamental unit of a neural network.
- Think of a vector as a column of numbers—for example, one column in a spreadsheet.
- Example: A vector might represent a set of features in your input data, like age, salary, and education level.
-
Matrices:
- When vectors are arranged side by side (column after column), they form a matrix.
- Matrices allow us to represent and process multiple data points simultaneously.For example, consider:
- A weight matrix that defines the connections between neurons in one layer and the next.
- An input vector representing data for a single instance.
- A matrix multiplication operation that applies the weights to the inputs, resulting in the outputs of the next layer.
- Linear Transformations:
- Neural networks apply linear transformations to data, represented as:
y=Wx+by
W: Weights matrix
x: Input vector
b: Bias vector
y: Output vector
- Activation Functions:Activation functions play a important role in neural networks by introducing non-linearity, enabling the network to model complex relationships and learn from data. Without activation functions, a neural network would behave like a linear regression model, regardless of the number of layers.
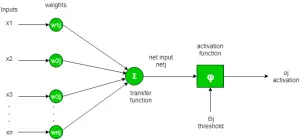
Why Do We Need Activation Functions?
- Non-linearity:
- Real-world data often involves non-linear patterns. Activation functions allow the network to capture these patterns.
- Feature Transformation:
- They transform the weighted sum of inputs into meaningful outputs for the next layer.
- Bounded Outputs:
- Some activation functions keep the outputs within a fixed range, improving stability during training.
After applying the linear transformation, the activation function modifies the output to introduce non-linearity.
- Non-linearity:
- Example: Using the ReLU function: ReLU(x)=max(0,x)
Why Linear Algebra?
Linear algebra provides the tools to efficiently compute the forward and backward passes in a neural network:
- Forward Pass: Propagates input data through layers to produce output.
- Backward Pass (Backpropagation): Computes gradients using matrices to optimize weights via techniques like gradient descent.
Bridging Neural Networks and Linear Algebra
From the above discussion, it becomes clear that understanding neural networks requires a strong grasp of linear algebra, particularly operations involving vectors and matrices. These concepts form the backbone of how data flows and computations occur within a neural network.
In subsequent articles, we will explore how these mathematical foundations are applied step-by-step to build and train a network, highlighting how real-world data is transformed into actionable outputs.
Check out more Blogs – Click here
Visit LinkedIn page – Click Here
